深入探究对数函数求导公式的奥秘与应用，对数函数求导公式的奥秘与应用深析

在数学的广袤领域中，函数求导是一项至关重要的技能，而对数函数作为常见的函数类型之一，其求导公式更是具有广泛的应用和深刻的内涵。

对数函数，通常以形如 \(y = \log_a x\) （\(a > 0\) 且 \(a \neq 1\)）的形式出现，对于以 \(a\) 为底的对数函数求导，其公式为：\((\log_a x)' = \frac{1}{x \ln a}\) 。

这个公式是如何推导出来的呢？我们以自然对数（即以 \(e\) 为底的对数，记为 \( \ln x\) ）为例来进行推导，设 \(y = \ln x\) ，\(x = e^y\) ，对 \(x = e^y\) 两边关于 \(x\) 求导，得到 \(1 = e^y \cdot y'\) ，即 \(y' = \frac{1}{e^y}\) ，而 \(e^y = x\) ，\(y' = \frac{1}{x}\) 。

对于一般底数 \(a\) 的对数函数 \(y = \log_a x\) ，我们可以利用换底公式将其转化为以 \(e\) 为底的自然对数形式，即 \(y = \frac{\ln x}{\ln a}\) ，然后求导可得：

\[

\begin{align*}

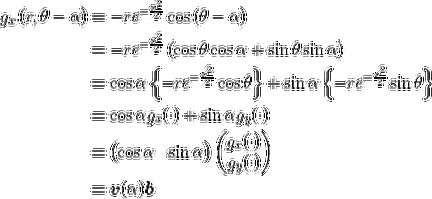
y'&=(\frac{\ln x}{\ln a})'\\

&=\frac{1}{\ln a} \cdot (\ln x)'\\

&=\frac{1}{x \ln a}

\end{align*}

\]

了解了对数函数求导公式的推导过程，接下来让我们看看它在实际中的应用。

在解决函数的单调性问题时，求导是常用的方法，通过对对数函数求导，可以判断其导数的正负，从而确定函数的单调区间。

在求解函数的极值和最值问题中，对数函数求导公式也发挥着重要作用，求出导数为零的点，再结合函数的单调性，就能找到极值点和最值。

在物理、工程、经济等领域的数学建模中，对数函数也经常出现，求导公式为分析和解决实际问题提供了有力的工具。

下面为大家解答几个与对数函数求导公式相关的问题：

问题一：求 \(y = \log_2 (x^2 + 1)\) 的导数。

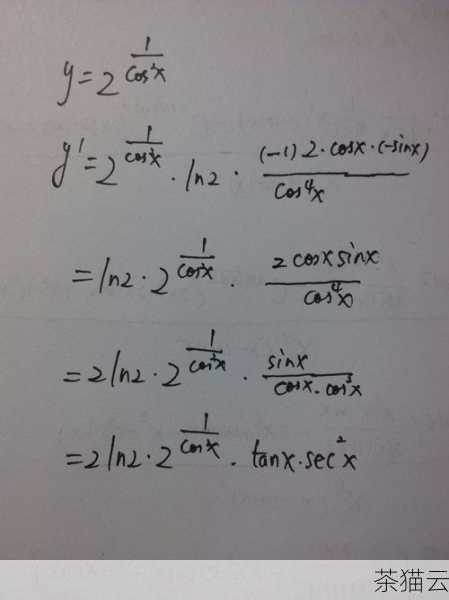
解：令 \(u = x^2 + 1\) ，则 \(y = \log_2 u\) 。

\(y' = (\log_2 u)' \cdot u'\)

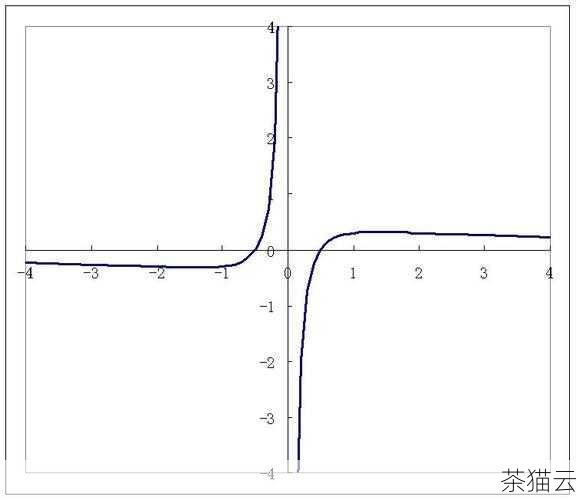
\((\log_2 u)' = \frac{1}{u \ln 2}\) ， \(u' = 2x\)

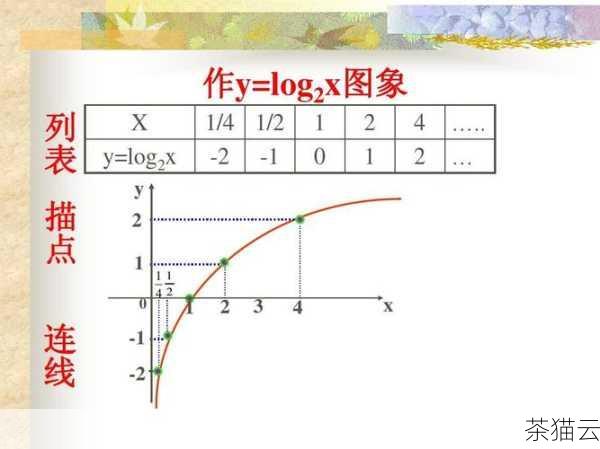
\(y' = \frac{2x}{(x^2 + 1) \ln 2}\)

问题二：已知 \(f(x) = \ln (x^3 - 2x + 1)\) ，求 \(f'(1)\) 。

解：首先求 \(f'(x)\) ， \(f'(x) = \frac{3x^2 - 2}{x^3 - 2x + 1}\)

则 \(f'(1) = \frac{3 - 2}{1 - 2 + 1} = \frac{1}{0}\) ，不存在。

问题三：求 \(y = \ln \sqrt{x}\) 的导数。

解：\(y = \ln \sqrt{x} = \frac{1}{2} \ln x\)

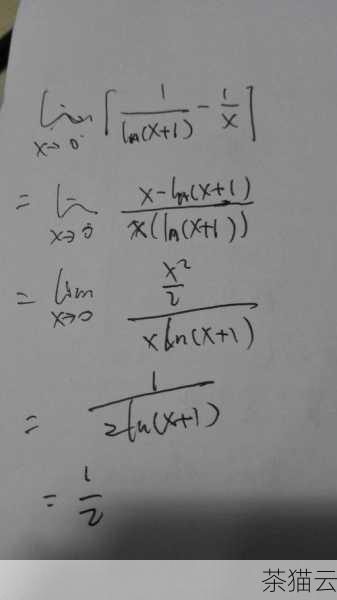
\(y' = \frac{1}{2} \cdot \frac{1}{x} = \frac{1}{2x}\)